The problem

When students learn to code FEM, they are usually not taught about sparse matrices. This is done to keep the code as well as the learning simple. Students are first taught how to code FEM, and then once they have to handle real problems, they are taught about sparse matrix operations. But unfortunately, most of the time, the semester ends without introducing sparse matrices, their importance and how to code them.

You can not even imagine solving medium to large-scale systems without sparse matrices.

Real world systems are usually somewhere between a few thousand to well over a million degrees of freedom (\(n\)). What this means is that the resulting matrix in the mathematical model of the system will be \(n \times n\). Luckily in the FEM, the matrices are usually sparse and we can solve for a big system. But most researchers do not understand how the size of the system is related to the computers ability to solve it.

background

Lets try to understand this:

  • Every number takes a certain amount of RAM space. Remember 1 byte = 8 bits and
Data Type Size Description
byte 1 byte -128 to 127
short 2 bytes -32,768 to 32,767
int 4 bytes -2,147,483,648 to 2,147,483,647
long 8 bytes -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807
float 4 bytes Stores fractional numbers. Sufficient for storing 6 to 7 decimal digits
double 8 bytes Stores fractional numbers. Sufficient for storing 15 decimal digits
boolean 1 bit Stores true or false values
char 2 bytes Stores a single character/letter or ASCII values

  • In general we work with double (8 bytes) data type to store data and with int (4 bytes) to store indexes.

  • 1MB = 1e6 Bytes

  • 1GB = 1e9 Bytes = 1000 MB

  • 1TB = 1e12 Bytes = 1000 GB

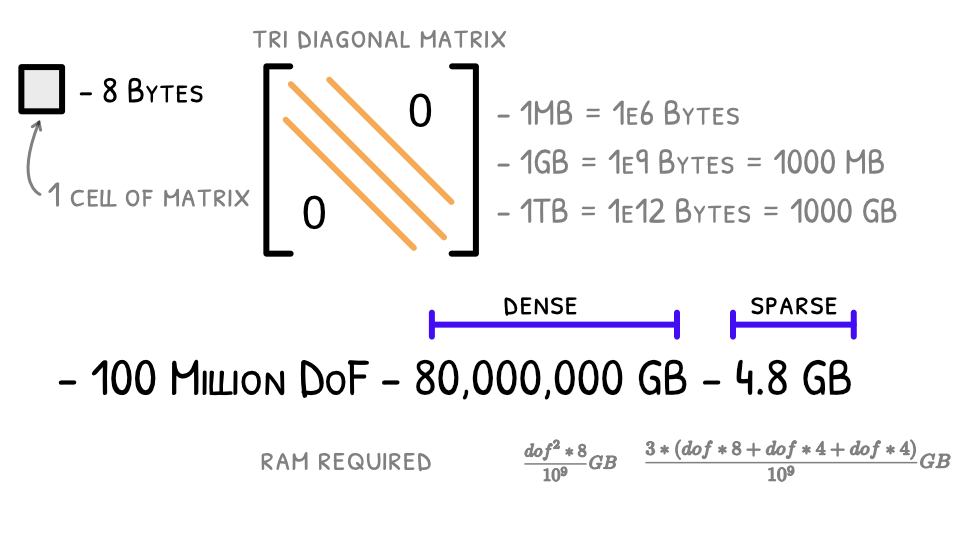
  • Considering a tridiagonal system where we have non zero entities only on the main diagonal and adjacent to it here is a comparison of RAM requirement for dense v/s sparse system.

    RAM for dense storage: \(\frac{dof^2 \times 8}{10^9}\)GB

    RAM for sparse storage: \(\frac{3 \times (dof \times 8+dof \times 4+dof \times 4)}{10^9}\)GB

    dof Num items RAM for Dense RAM for Sparse
    1000 1 Million 8 MB 0.048 MB
    10,000 1e8 800 MB 0.48 MB
    1 Lakh 1e10 80 GB šŸ§ 4.8 MB
    1 Million 1e12 8 TB šŸ˜Ø 48 MB
    10 Million 1e14 800 TB šŸ˜± 480 MB
    100 Million 1e16 0.8 Million TB šŸ¤Æ 4.8 GB
    1 Billion 1e18 80 Million TB ā˜ ļø 48 GB

  • The above table is formed by considering that every cell of the matrix will hold a double value (8 bytes) and the indices are stored as integers (4 bytes) for the sparse matrix. A sparse matrix is stored as a 3 column matrix with first column being data the second being row number and the third being column number.

  • Thus you can see that by using a dense matrix you will exhaust you laptop memory even with a 1Lakh dof system.

The solution

If you are a researcher working with matrices, you should learn and understand how to work with sparse matices. It is the only way to solve large systems on your computer. There is no other alternative.

  • You can find the code for this blog here
  • Start learning about sparse matrix algebra here and here

References