In FEniCS there are three different kinds of function space which we can use.

FS = FunctionSpace(mesh, "CG", 1)
VFS = VectorFunctionSpace(mesh, "CG", 1)
TFS =  TensorFunctionSpace(mesh, "CG", 1)

As the name implies:

• FunctionSpace is to define scalar functions over the mesh and have one value per vertex.
• VectorFunctionSpace is used to define vectors over the mesh and have $d$ values over the vertex where $d$ is the dimension of the problem. Thus in one dimension it will return a scalar, but it is necessary to define the quantities such as gradients on VectorFunctionSpace which are vectors in 2D and 3D.
• TensorFunctionSpace is used to define tensor functions over the mesh.

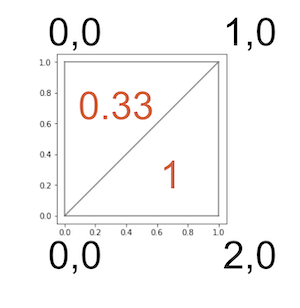
In this post I am going to talk about FunctionSpace and VectorFunctionSpace that I mostly use to define scalar or vector fields over the mesh. Suppose, I have the following mesh which is discretized with traingular elements haveing two degrees of freedom at each node.

This mesh is generate with the help of following commands

from dolfin import *
%matplotlib inline
mesh = UnitSquareMesh(1,1)

Next, we define the displacement vector field over the mesh. This could be achieved by first defining a VectorFunctionSpace and then defining the Functionover the function space.

VFS = VectorFunctionSpace(mesh, "CG", 1)
unew, uold = Function(VFS), Function(VFS)

We can then manually define the vector field based on custom data. Under the hood - ignoring all the complex methods present in the function - a fucntion contains the values of the field at the degrees of freedom in the order

$$[x_0,y_0,x_1,y_1,x_2,y_2 ... , x_n, y_n]$$

where $n$ is the degree of freedom number. In the above mesh we have 2 degrees of freedom per vertex. Thus, we can modify the vectors

unew.vector().vec().array = np.array([0,0,0,0,1,0,2,0])
uold.vector().vec().array = np.array([0,0,0,0,0,0,0,0])

We can then find the error field over the mesh. Now, since we are finding the error between two vector fields the error will also be a vector field.

error_u = project(unew-uold,VFS)

The vector error_u will contain two values at each vertex, one for error in x and other for error in y. We can check the values by using the method compute_vertex_values

error_u_x, error_u_y = error_u.split()
error_u_x.compute_vertex_values()
error_u_y.compute_vertex_values()

Now, I want the magnitude of the error at each vertex. For this I can write an expression in UFL for magnitude and then project that to a FunctionSpace since I want a single value per vertex

FS = FunctionSpace(mesh, 'CG', 1)
error_u_mag = project(sqrt(inner(error_u,error_u)),FS)

This will give me a field containing the magnitude of the error at each vertex, now to average the error over each element I can take help of Discontinuous Galerkin element

DG = FunctionSpace(mesh, "DG", 0)
error_u_mag_cell =interpolate(error_u_mag,DG)
error_u_mag_cell.vector()[:]

Out: array([ 1. , 0.33333333])

This way I will get the error magnitude over each cell in the mesh.